Las leyes de Newton, también conocidas como leyes del movimiento de Newton,1 son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la mecánica, en particular, aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo, en tanto queconstituyen los cimientos no sólo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones... La validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.
Primera ley de Newton o Ley de la inercia
La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.5
Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.Segunda ley de Newton o Ley de fuerza
La segunda ley del movimiento de Newton dice que:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.6
Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.
En términos matemáticos esta ley se expresa mediante la relación:
Donde:
 es el momento lineal
es el momento lineal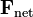 la fuerza total o fuerza resultante.
la fuerza total o fuerza resultante.
Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz7 la ecuación anterior se puede reescribir de la siguiente manera:
Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
 es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.
Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:
 aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior:Tercera ley de Newton o Ley de acción y reacción Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.6
La tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.8 Expone que por cada fuerza que actúa sobre un cuerpo (empuje), este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto.
Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.


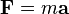
 o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio,
, entonces un polinomio,  , de grado n en la variable x es un objeto de la forma
, de grado n en la variable x es un objeto de la forma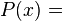



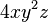 es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.